Vstupte do světa „Simpsnovi Cosine: Cosine a Jeho Matematické Dobrodružství“, kde se matematika stává nejen výzvou, ale i zábavou! Představujeme vám fascinující příběh, který spojí vzrušující dobrodružství a trigonometrii do jednoho šíleného mixu. Pokud jste někdy přemýšleli, jak by to vypadalo, kdyby se geometrické tvary rozhodly uspořádat vlastního Superhrdinu, pak je „Simpsnovi Cosine: Cosine a Jeho Matematické Dobrodružství“ právě to, co potřebujete. Ponořte se do napínavých zápasů, naučte se, jak pojmenovat synonymní úhly, a objevte, proč se Cosine rozhodl pro svou jedinečnou cestu motivačního růstu! Uvidíte, že i v nejobtížnějších matematických úlohách se skrývá humor a úžasné zážitky. Tak se pohodlně usaďte a připravte se na výlet, který vám ukáže, že matematika může být nejen přesná, ale i neuvěřitelně zábavná!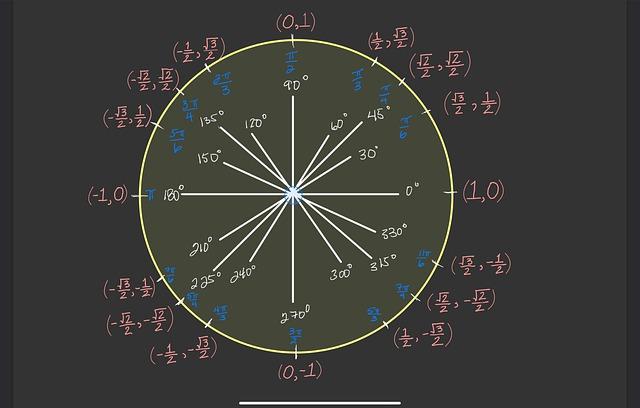
Obsah
- Simpsnovi Cosine a jeho význam v trigonometrii
- Základy kosinové funkce a její historie
- Praktické aplikace kosinové funkce v reálném světě
- Matematické dobrodružství s grafem funkcí
- Jak efektivně používat kosinus v příkladech
- Nejčastější chyby při práci s kosinovou funkcí
- Tipy a triky pro zapamatování kosinových vlastností
- Pokročilé úvahy o kosinových identitách
- Budoucnost trigonometrii v moderní matematice
- Doporučené zdroje pro další studium kosinusových funkcí
- Otázky & Odpovědi
- Klíčové Poznatky
- Simpsnovi Elizabeth Hooverová: Učitelka Lisy Simpsonové
- Co Homer Simpson rád jí? Top 10 oblíbených jídel Homera!
- Kdy Zemřel Bart Simpson? Šokující Zvrat v Seriálu
- Kdy skončí Simpsonovi? Budoucnost seriálu!
Simpsnovi Cosine a jeho význam v trigonometrii
V světě trigonometrije hraje **Simpsnovi Cosine** klíčovou roli při pochopení vztahů mezi úhly a stranami různých geometrických tvarů. Tento koeficient, představující poměr přilehlé strany k přeponě v pravoúhlém trojúhelníku, nám poskytuje užitečné nástroje k analýze a výpočtům v mnoha oblastech matematiky a fyziky. Pomocí kosinové funkce můžeme snadno vyřešit úlohy související s osami, polaritami a dokonce i vlnovými pohyby. Mezi základní vlastnosti patří:
- Periodicita: Funkce má periodu 360° nebo 2π radiánů.
- Úhly: Vztahuje se k úhlům od 0° do 180° a zpět, je to funkce sudá.
- Interval: Hodnoty se pohybují v rozmezí od -1 do 1.
V praxi se Simpsnovi Cosine často využívá při výpočtech v trojúhelníkových aplikacích, jako jsou určení délek stran pomocí **kosinové věty**. Tato věta poskytuje silný nástroj pro získání informací o nezávislých délkách stran bez nutnosti měřit úhly přímo. Její účinnost je obzvlášť viditelná v oblastech, jako jsou navigace, architektura a dokonce i v oblasti inženýrství. Příklady aplikací zahrnují:
- Architektonické návrhy: Použití pro výpočty sklonů a úhlů střech.
- Navigační systémy: Umožňuje efektivní výpočet tras a vzdáleností.
- Fyzika: Analýza sil a směrování ve vektorových prostorech.
Základy kosinové funkce a její historie
Kosinusová funkce, označovaná jako cos, je klíčový prvek trigonometrii, který popisuje vztah mezi délkou přilehlé strany a přeponou v pravoúhlém trojúhelníku. Tato funkce je důležitá nejen v geometrii, ale i v mnoha dalších oblastech matematiky a fyziky. Historicky se kosinus vyvinul ze snah astronomů a matematiků starověkého Řecka a Indie, kteří se zabývali studiem cyklických pohybů a úhlů. Je fascinující, jak se kosinusová funkce postupně transformovala od jednoduchých geometrických konceptů až po sofistikované analytické metody, které používáme dnes.
Mezi základní vlastnosti kosinové funkce patří její periodicita, která vyjadřuje opakování hodnoty kosinu každých 360° nebo 2π radiánů. Tím pádem můžeme vyjádřit kosinus pomocí řešení následující tabulky:
| Kosinus | |
|---|---|
| 0° | 1 |
| 30° | √3/2 |
| 60° | 🧈 |
| 90° | 0 |
Tyto hodnoty mají zásadní význam pro mnoho aplikací, od návrhu silnic a mostů po analýzu vlnových jevů v přírodě. Nezáleží na oblasti použití; kosinusová funkce nám vždy poskytuje cenné informace a nástroje pro modelování a pochopení světa kolem nás.
Praktické aplikace kosinové funkce v reálném světě
Kosinová funkce má v reálném světě široké využití, které sahá od architektury až po hudbu. V architektuře se kosinové funkce využívají při analýze a návrhu zakřivených struktur, kde je důležité správně interpretovat křivosti a úhly světla. Například, když architekti navrhují budovy s neobvyklými tvary, používají kosinové funkce k určení, jak se budou jednotlivé části konstrukce vzájemně ovlivňovat. V hudbě hrají kosinové funkce klíčovou roli při syntéze zvuku, kdy se signály kombinují a modifikují pro vytváření harmonických tónů a rytmů.
Dalším zajímavým příkladem praktického použití kosinové funkce je analýza periodických jevů, jako jsou vlnění nebo cyklické trendy v ekonomice. Ve fyzice a inženýrství se používají kosinové funkce k modelování pohybů, například při zkoumání vibrací strojů nebo chování oscilátorů. Nezanedbatelný je také jejich význam v oblasti strojového učení a datové analýzy, kde se často využívá pro transformaci signálů a rozpoznávání vzorů. Díky těmto aplikacím se ukazuje, že kosinové funkce nejsou pouze abstraktními matematickými nástroji, ale silnými nástroji pro řešení praktických problémů.
Matematické dobrodružství s grafem funkcí
Graf funkce cosinus nám otevírá fascinující svět trigonometrije, kde se spojují geometrie a analýza. Pokud se na něj podíváme, zjistíme, že periodické vlastnosti této funkce vytvářejí krásné vlny, které se opakují každých 360°. Tyto vlny se dají skvěle využít v různých oblastech, jako jsou fyzika, inženýrství nebo dokonce ve zvukové produkci. Abychom lépe pochopili, jak funkce cosinus funguje, můžeme si připravit jednoduchý graf. Ten nám hned ukáže, jak se hodnoty cosinu mění v závislosti na úhlovém měření:
| Úhel (°) | Cosinus |
|---|---|
| 0 | 1 |
| 90 | 0 |
| 180 | -1 |
| 270 | 0 |
| 360 | 1 |
Samotná funkce se dá také skvěle ilustrovat pomocí různých aplikací, které přibližují její reálné využití. Například, jakmile použijeme cosinus v různých praktických scénářích, jako je analýza harmonických pohybů nebo dokonce i v uměleckém vyjádření, vidíme, jak matematika oživuje každodenní situace. Zajímavé je, že pokud se pustíme do objekty, které se otáčejí kolem osy, kosinus nám pomáhá porozumět jejich trajektoriím: od výpočtu vzdálenosti po určení úhlové rychlosti, až po simulaci různých pohybových vzorců. V grafech se tak odráží nejen teorie, ale i naše kreativita ve světě čísel a prostorových vztahů.
Jak efektivně používat kosinus v příkladech
Kosinus je v matematice jednou z nejdůležitějších funkcí, zejména při práci s trojúhelníky a v trigonometrických výpočtech. Při použití kosinu bychom měli mít na paměti několik klíčových bodů:
- Definice: Kosinus úhlu je poměr mezi délkou přilehlé strany a délkou přepony v pravoúhlém trojúhelníku.
- Aplikace: V praxi se kosinus používá při výpočtu vzdáleností, statice a dynamice, či dokonce při analýze vlnových jevů.
- Vztahy: Vztah kosinu k jiným trigonometrickým funkcím, jako je sinus a tangens, může vést k efektivnějším řešením komplexních úloh.
Jedním z praktických příkladů využití kosinu může být výpočet délky stínové části budovy. Pokud známe úhel sklonu slunce a výšku budovy, můžeme použít kosinus k určení délky stínu. Můžeme to shrnout do jednoduché tabulky:
| Úhel sklonu (v °) | Výška budovy (m) | Délka stínu (m) |
|---|---|---|
| 30 | 10 | 17.32 |
| 45 | 10 | 10.00 |
| 60 | 10 | 5.00 |
Přesné hodnoty délky stínu samozřejmě závisí na specifické situaci a úhlu slunce, ale tento princip dokazuje, jak užitečný může být kosinus ve výpočtech v reálném světě.
Nejčastější chyby při práci s kosinovou funkcí
Při práci s kosinovou funkcí se často setkáváme s několika častými chybami, které mohou vést k nesprávným výsledkům a frustraci. Jednou z nejčastějších chyb je neporozumění úhlu měřeného v radiánech a stupních. Mnoho studentů mylně předpokládá, že kosinovou funkci lze použít stejným způsobem bez ohledu na to, v jakých jednotkách je úhel vyjádřen. Vždy je důležité si být vědom toho, jaký formát používáme a podle toho upravit naše výpočty nebo hodnoty, které z této funkce získáváme.
Další obvyklou chybou je ignorování periodičnosti kosinové funkce. Kosinová funkce je periodická, což znamená, že její hodnoty se opakují po každém celém násobku 360° (nebo 2π radianů). To může vést k situacím, kdy si uživatelé myslí, že získali unikátní hodnotu, zatímco ve skutečnosti existují další hodnoty, které odpovídají stejnému výsledku. V následující tabulce je uvedena základní periodičnost kosinové funkce:
| Úhel (stupně) | Kosinus |
|---|---|
| 0° | 1 |
| 90° | 0 |
| 180° | -1 |
| 360° | 1 |
Tipy a triky pro zapamatování kosinových vlastností
Zapamatování kosinových vlastností může být pro mnoho studentů výzvou, ale s pár užitečnými tipy a triky to jde mnohem jednodušeji. Zde je několik technik, které vám pomohou lépe si osvojit tyto matematiké koncepty:
- Vizualizace: Představte si kosinovou křivku a její vlastnosti. Kreslení grafů a jejich analýza vás navede na správnou cestu.
- Pravidelný trénink: Cvičte pravidelně, abyste si upevnili znalosti. Mějte k dispozici pracovní sešity nebo online platformy, které nabízejí úlohy k procvičení.
- Zapamatovací pomůcky: Vytvořte si akronymy pro zapamatování klíčových vzorců, jako je jednotková kružnice, nebo si napište vtipné rýmy.
Další možností, jak si usnadnit zapamatování, je vytvoření jednoduché tabulky, která shrnuje základní kosinové vlastnosti. Taková tabulka vám umožní rychle se podívat na důležité informace a lépe je pochopit:
| Vlastnost | Formule |
|---|---|
| Shodnost kosinů (pro vektory) | cos(A + B) = cosA * cosB – sinA * sinB |
| Oddělení úhlů | cos(2A) = cos²A – sin²A |
| Kosinová věta | c² = a² + b² – 2ab * cos(C) |
Pokročilé úvahy o kosinových identitách
V oblasti trigonometie hrají kosinové identity klíčovou roli, zvlášť při řešení různých matematických problémů a důkazech. Mezi nejznámější patří základní identita ( cos^2(theta) + sin^2(theta) = 1 ), která nám umožňuje spojit kosinus a sinus jakékoliv úhlu. Tento vztah není jen teoretický; má praktické využití v oborech jako je fyzika či inženýrství, kde se často modelují oscilace a vlny. Další důležité identitní vztahy zahrnují dvojité úhly, například ( cos(2theta) = cos^2(theta) – sin^2(theta) ), což usnadňuje práci při analýze komplexních trigonometrických funkcí a geometrických úloh.
Abychom lépe porozuměli těmto identitám, můžeme se podívat na vizualizaci různých funkcí a jejich interakcí. **Grafickým znázorněním** kosinové funkce a jejích identit si můžeme ověřit, jak se mění hodnoty při různých úhlech. Dále se vyplatí zamyslet nad **aplikacemi** kosinových identit v praktických situacích, jako jsou náklony ramp či výpočty výšek objektů pomocí stínů. Tyto vztahy nám umožňují lépe porozumět nejen abstraktní matematice, ale i reálným problémům, s nimiž se setkáváme v každodenním životě.
Budoucnost trigonometrii v moderní matematice
Trigonometrii se podařilo přežít i v moderním matematickém světě díky svému neustálému přizpůsobování a inovacím. S nástupem nových technologií a zvýšeným důrazem na datovou analýzu se geometrické a trigonometrijské koncepty stávají stále důležitějšími. **Výpočetní trigonometrie** se dnes používá v oblastech od počítačové grafiky po modelování fyzikálních jevů. Tento přístup navíc umožňuje kombinaci trigonometrických funkcí s jinými matematickými disciplínami, čímž vznikají nové fascinující teorie a aplikace. Důležitost těchto znalostí nelze podceňovat, protože poskytnou matematickou a logickou základnu pro pochopení komplexnějších systémů.
vypadá slibně, protože se objevují nové výzkumné oblasti, které zahrnují **kombinatorní trigonometrie** a analýzu periodicity. Následující tabulka uvádí některé z klíčových a aktuálních aplikací trigonometrii v různých oblastech:
| Aplikace | Popis |
|---|---|
| Počítačová grafika | Animace a rendering pomocí trigonometrických funkcí pro realistické vizualizace. |
| Fyzika | Modelování vlnění a oscillace, jako jsou melodie a zvuky. |
| Architektura | Design budov a struktury, které využívají trigonometrické vzory pro stabilitu. |
| Informatika | Algoritmy pro zpracování signálů a analýzu dat v oblastech jako strojové učení. |
Doporučené zdroje pro další studium kosinusových funkcí
Pro ty, kteří se chtějí do hloubky ponořit do tajů kosinusových funkcí, je zde několik doporučených zdrojů, které vám mohou pomoci. **Knihy** jsou stále jedním z nejlepších způsobů, jak získat strukturované a podrobné znalosti. Doporučujeme zejména tyto tituly:
- „Matematika pro středoškoláky“ od Jana Nováka
- „Funkce a jejich aplikace“ od Marie Hruškové
- „Trigonometry Simplified“ od Petera Diplomata
Pokud preferujete online zdroje, můžete navštívit několik užitečných webových stránek a videí. **Interaktivní platformy** jako Khan Academy nebo Coursera nabízejí kurzy zaměřené na trigonometrii a kosinusové funkce. Další skvělou volbou jsou YouTube kanály, například “Mathologer” nebo “3Blue1Brown”, které vizuálně ilustrují koncepty, což vám pomůže lépe pochopit, jak a proč kosinusové funkce fungují. Pro shrnutí, zde je tabulka doporučených online platforem a jejich zaměření:
| Platforma | Typ Obsahu |
|---|---|
| Khan Academy | Interaktivní kurzy |
| Coursera | Akatemické kurzy |
| YouTube | Vizuální materiály |
Otázky & Odpovědi
Q&A K Článku „Simpsnovi Cosine: Cosine a Jeho Matematické Dobrodružství“
Otázka 1: O čem je článek „Simpsnovi Cosine“?
Odpověď: Článek se zaměřuje na fascinující příběh matematické funkce cosinus, přičemž sleduje její historický vývoj, aplikace a význam v různých oblastech matematiky a vědy. Hlavní postavou je personifikovaný Simpsnovi Cosine, který provádí čtenáře dobrodružstvím světem trigonometrie.
Otázka 2: Jaké historické souvislosti článek zmiňuje?
Odpověď: Článek se dotýká kořenů trigonometrie, počínaje starověkými civilizacemi jako Babylon nebo Řecko, kde byly první formy trigonometrických funkcí formulovány. Popisuje také význam jednotlivých matematiků jako Hipparchos a Ptolemaios, kteří přispěli k pochopení těchto funkcí.
Otázka 3: Jaké praktické aplikace cosinu článek prezentuje?
Odpověď: V článku se objasňuje, jak se funkce cosinus využívá v různých oblastech, jako je fyzika při studiu vlnění a harmonických oscilací, architektura, kde pomáhá při navrhování budov, a dokonce i v moderní technologii jako je počítačová grafika.
Otázka 4: Co je na článku nejzajímavější?
Odpověď: Nejzajímavější je interaktivní přístup, kterým článku vkládá do příběhu humor a osobní pohledy Simpsnovi Cosine. Čtenáři si mohou lépe představit, jak trigonometrie ovlivňuje náš každodenní život a jak se bez ní neobejdeme, a to vše zábavnou formou.
Otázka 5: Je článek určen pouze pro odborníky na matematiku?
Odpověď: Rozhodně ne. Článek je napsán tak, aby byl přístupný široké veřejnosti. I když se dotýká odborných témat, používá jasný a srozumitelný jazyk, takže si ho mohou užít i ti, kteří nejsou matematikům blízcí.
Otázka 6: Jak může čtenář pokračovat v objevování trigonometrie po přečtení tohoto článku?
Odpověď: Čtenář může prohloubit své znalosti pomocí doporučené literatury a online kurzů o trigonometrii a matematice obecně. Článek obsahuje také odkazy na užitečné zdroje, kde najdou další informace a praktické úkoly pro cvičení svých dovedností.
Otázka 7: Kde a kdy si mohu článek přečíst?
Odpověď: Článek „Simpsnovi Cosine: Cosine a Jeho Matematické Dobrodružství“ je k dispozici online na našem webu a můžete si ho přečíst kdykoliv. Doporučujeme si udělat pauzu a ponořit se do světa matematiky, když máte chvilku na přemýšlení.
Otázka 8: Bude v budoucnu víc podobných článků?
Odpověď: Ano, plánujeme pokračovat v sérii článků, které budou zkoumat další důležité matematické koncepty a jejich příběhy. Rádi bychom, aby se matematika stala pro čtenáře ještě fascinující a přístupnější.
Klíčové Poznatky
Ať už jste se do této fascinující cesty matematikou ponořili jako nováčci, nebo jste již zkušenými matematiky, příběh Simpsnovi Cosine a jeho dobrodružství s kosinovými funkcemi nás všechny může inspirovat. Matematiky nejsou jen suché rovnice a čísla; jsou to příběhy, které nám pomáhají porozumět světu kolem nás.
Jak jsme viděli, kosinová funkce není pouhým nástrojem pro výpočty, ale klíčovým prvkem, který odhaluje hloubku a krásu geometrie a trigonometrie. Ponořte se hlouběji do tajemství těchto funkcí, neboť každé dobrodružství má své nekonečné možnosti objevování.
Doufáme, že vás tento článek inspiroval k dalšímu zkoumání matematických konceptů a k jejich aplikaci v reálném světě. Nezapomeňte, že matematika je nejen o číslech, ale i o nalézání spojení a porozumění vzorům, které utvářejí náš každodenní život. Pokračujte v objevování a vězte, že vaše vlastní dobrodružství s matematikou teprve začíná!